Wiskundetaal
Oppervlakte, eenheid, vierkante meter, vierkante decimeter, vierkante centimeter (landmaten, are, hectare, centiare)
Eindtermen
ET 2.1 De leerlingen kennen de belangrijkste grootheden en maateenheden met betrekking tot lengte, oppervlakte, inhoud, gewicht(massa) tijd, snelheid, temperatuur en hoekgrootte en ze kunnen daarbij de relatie leggen tussen de grootheid en de maateenheid.
ET 2.2 De leerlingen kennen de symbolen, notatiewijzen en conventies bij de gebruikelijke maateenheden en kunnen meetresultaten op veelzijdige wijze noteren en op verschillende wijze groeperen.
ET 2.3 De leerlingen kunnen veel voorkomende maten in verband brengen met betekenisvolle situaties.
ET 2.6 De leerlingen kunnen allerlei verbanden, patronen en structuren tussen en met grootheden en maatgetallen inzien en ze kunnen betekenisvolle herleidingen uitvoeren.
ET 2.7 De leerlingen kunnen met de gebruikelijke maateenheden betekenisvolle herleidingen uitvoeren.
ET 2.8 De leerlingen kunnen schatten met behulp van referentiepunten.
ET 2.9 De leerlingen kunnen op een concrete wijze aangeven hoe ze de oppervlakte en de omtrek van een willekeurige, vlakke figuur en van een veelhoek kunnen bepalen.
Basis
- Werk rond referentiematen, laat leerlingen bv. de juiste eenheid combineren met een maatgetal (bv. de oppervlakte van mijn werkboek is 6 …).
- Werk rond basisherleidingen met de gekende eenheden.
- Combineer de herleidingsopgaven ook met breuken (bv. ½ m2 = … dm2).
- Combineer de herleidingsopgaven met referentiematen door de komma op de juiste plaats te laten zetten (bv. plaats de komma zodat het klopt: de oppervlakte van de smartphone is 112 dm2).
- Geef opdrachten waarbij leerlingen moeten herleiden om de oppervlakte te vergelijken (bv. duid aan welke oppervlakte het grootst is: 120 cm2 of 1,5 dm2).
- Laat de oppervlakte van een figuur berekenen. Neem zowel ‘gekende veelhoeken’ waarbij ze een formule kunnen toepassen als figuren waar ze moeten omstructureren (bv. verdelen in figuren waarvan ze de oppervlakte wel kunnen berekenen via de gekende formules). In de derde graad komt hier ook de oppervlakte van ruimtefiguren (bv. balk) bij. Besteed aandacht aan de notatie van de eenheden.
- Laat vanuit de oppervlakte een bepaalde afmeting bepalen (bv. vanuit de oppervlakte en de lengte van een rechthoek de breedte berekenen).
- Laat leerlingen zelf contexten bedenken bij het begrip oppervlakte (bv. hoeveel verf nodig, hoeveel zaad voor grasveld, oppervlakte woning,…), gebruik het begrip in combinatie met ‘omtrek’ om het verschil uit te klaren.
- Laat leerlingen een figuur met een bepaalde oppervlakte tekenen.
Toepassingen
Tim maakt een schets van de nieuwe voortuin. Op de niet verharde oppervlakte wil hij bodembedekkers planten. Hoeveel oppervlakte is voorzien voor bodembedekkers?
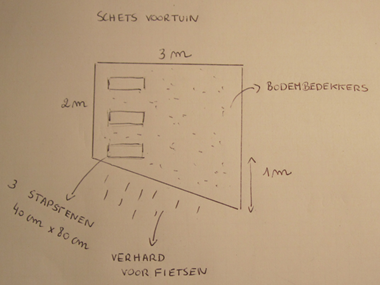
Tip: Pas de complexiteit van de figuur aan naargelang de voorkennis van de leerlingen en de oppervlakteberekening die je wil inoefenen. Je kan uiteraard ook de ‘stapstenen’ of andere zaken binnen de figuur weglaten. Je kan ook werken met aanleg speeltuin, park, terras,.. Combineer eventueel met de kostprijs van bodembedekkers, tegels, graszaad,…
- Bespreek op welke manier ze de totale oppervlakte berekend hebben – bv. door het tuintje te zien als de combinatie van een rechthoek met een driehoek, of van een vierkant waar een driehoek van weggehaald is.
- Besteed aandacht aan de herleiding die hier nodig is om de oppervlaktes af te trekken: de totale oppervlakte van het tuintje is 7,5 m2, de oppervlakte van de stapstenen zal dus ook uitgedrukt moeten worden in vierkante meter om het verschil te kunnen berekenen.
- Laat leerlingen bij elkaar bekijken op welke manier ze dit genoteerd hebben. Het overzichtelijk noteren van de tussenstappen is hier belangrijk. Laat ook bekijken of ze aanduidingen gemaakt hebben op de figuur om het rekenwerk te ondersteunen.
- Bespreek of een schatting of een heel precies resultaat hier het meest zinvol is. Zo zou je de oppervlakte van de drie stapstenen samen kunnen benaderen door 1 vierkante meter.
- Laat op basis van deze toepassing een aantal contexten bedenken waar het nodig is om oppervlakte te berekenen (bv. terrastegels, beplanting).
De overheid raadt aan om minstens 8 m2 speelplaats te voorzien per leerling. Op basisschool ‘De speelvogels’ heeft de speelplaats afmetingen 25 m x 40 m. Er spelen tijdens de middagspeeltijd 200 kinderen. Hebben ze voldoende speelruimte volgens de richtlijn van de overheid?
Tip: pas de context aan de gegevens van je school aan.
- Laat de betekenis van de richtlijn verwoorden: het is niet de bedoeling dat elke leerling op 8 m2 speelt, het is een richtlijn voor de totale oppervlakte.
- Ga in op het resultaat – verschilt het veel van de richtlijn? Hoeveel groter zou de speelplaats moeten zijn? Bekijk in verhouding, in het voorbeeld is er een oppervlakte van 1000 m2 voorzien terwijl er 1600 m2 nodig is, de speelplaats zou dus met ruim de helft moeten vergroten.
Deze wandtegel heeft afmetingen 20 cm x 25 cm.
Voor een pakket met 30 van deze tegels betaal je 15 euro.
Hoeveel kosten deze tegels per vierkante meter?

- Deze opgave is beknopt geformuleerd, laat leerlingen navertellen in eigen woorden.
- Besteed aandacht aan het overzichtelijk noteren van de tussenstappen bij deze opgave. Bekijk met de leerlingen hoe de notatie duidelijker wordt, bv. door het noteren van ‘tussentitels’ zoals ‘oppervlakte 1 tegel’, ‘oppervlakte 30 tegels’, ‘prijs per vierkante meter’.
Op de speelplaats staat deze mini-plantentuin.
Bepaal de oppervlakte van deze plantentuin als je weet dat elk deeltje een vierkant is met zijde 30 cm.

- Bespreek de verschillende oplossingsmethodes.
> Je kan de oppervlakte van één klein vierkant berekenen (30 cm x 30 cm), en dan vermenigvuldigen met 16.
> Je kan de zijde van het tuintje berekenen (4 x 30 cm), en dan de totale oppervlakte.
- Bespreek de eenheid waarin het resultaat uitgedrukt wordt. Welke eenheid is interessantst om een idee te krijgen van de oppervlakte? (vierkante meter, want als je de oppervlakte uitdrukt in bv. vierkante centimeter krijg je een getal met veel nullen).
- Vergelijk met de referentiemaat voor één vierkante meter. Kan het resultaat?
Bepaal de oppervlakte van deze figuur. De verpakking is 30 cm lang.
De zijde van de driehoek is 4,5 cm. De verpakking is 4 cm hoog.

Pas de opgave aan, werk met een verpakking die je zelf meebrengt.
- Laat de leerlingen bij elkaar kijken op welke manier ze de werkwijze genoteerd hebben. Bij deze opgave is het overzichtelijk noteren van tussenstappen heel belangrijk.
- Het noteren van de afmetingen op de figuur is hier een zinvolle aanpak – zet dit in de verf.
- Laat de figuur benoemen met de correcte terminologie (ruimtefiguur, veelvlak).