Wiskundetaal
Vlakke figuur, veelhoek, regelmatige veelhoek, driehoek, gelijkbenige driehoek, ongelijkbenige driehoek, gelijkzijdige driehoek, scherphoekige driehoek, rechthoekige driehoek, stomphoekige driehoek, vierhoek, vierkant, rechthoek, ruit, parallellogram, trapezium, zijde, overstaande zijde, evenwijdig, loodrecht, diagonaal, cirkel
Ruimtefiguur, veelvlak, niet-veelvlak, kubus, balk, bol, cilinder, kegel, ribbe, grondvlak, zijvlak, ontvouwing (ontplooiing, ontwikkeling)
Eindtermen
ET 3.2 De leerlingen kunnen op basis van volgende eigenschappen de volgende meetkundige objecten herkennen en benoemen :
a) in het vlak : punten, lijnen, hoeken en vlakke figuren (driehoeken, vierhoeken, cirkels);
b) in de ruimte : veelvlakken (kubus, balk, piramide) en bol en cilinder.
ET 3.4 De leerlingen kunnen de verschillende soorten hoeken classificeren en de verschillende soorten vierhoeken classificeren op grond van zijden en hoeken. Zij kunnen deze ook concreet vormgeven.
Basis
- Toon een figuur (een vlakke figuur of een ruimtefiguur) en laat de juiste naam noteren. Als leerlingen de classificatie al gezien hebben kan je alle passende namen laten geven (bv. je toont een balk, leerlingen benoemen deze figuur als ruimtefiguur, veelvlak, balk). Werk ook met afbeeldingen en voorwerpen uit de realiteit (bv. een verpakking). Laat in de bespreking de kenmerken van de figuur verwoorden. Je kan eventueel ook vragen om die tijdens het werkmoment te noteren, of je kan de leerlingen de passende eigenschappen laten aanduiden in een lijst eigenschappen.
- Laat een figuur tekenen (bv. teken een ruit), geef eventueel bijkomende eisen qua afmetingen (bv. teken een parallellogram met hoogte 3 cm, bv. teken een gelijkbenige driehoek met basis 5 cm, bv. teken een ruit met diagonalen van 5 cm en 3 cm). Bruikbare werkvorm: Geef elke leerling een kaartje met de naam van een figuur op (bv. ‘gelijkbenige, stomphoekige driehoek’). Zorg dat duo’s een verschillend kaartje hebben. Laat leerlingen de figuur die op hun kaartje vermeld staat tekenen, de duopartner geeft daarna de naam van de getekende figuur, het kaartje is de correctiesleutel.
- Geef een aantal eigenschappen van een figuur en laat leerlingen de naam van de figuur zoeken (bv. Ik ben een vierhoek met drie rechte hoeken. Welke figuur kan ik zijn?).
- Laat een deel van een figuur zien en vraag welke figuur verstopt kan zitten. (bv. bij de figuur hieronder: Welke vierhoek kan dit zijn? Geef alle mogelijkheden.)
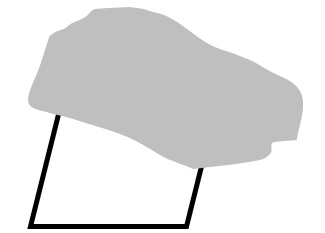
- Eens leerlingen de classificatie gezien hebben kan je werken met ‘denkoefeningen’ bv. ‘Zijn alle stomphoekige driehoeken gelijkbenig?’, bv. ‘Is elk vierkant een ruit?’
- Ontwikkelingen van ruimtefiguren kan je laten oefenen door te laten oordelen of een ontwikkeling bij een bepaalde figuur kan horen of niet. Zorg ervoor dat je de ontwikkeling ook effectief bijhebt om tijdens de bespreking te gebruiken.
Toepassingen
In de figuur hieronder zie je een ‘tangram’. Dat is een oude Chinese puzzel die bestaat uit 7 stukken. Je kan er heel veel figuren mee maken.
Welke vorm hebben de verschillende stukken? Geef telkens de best passende naam.
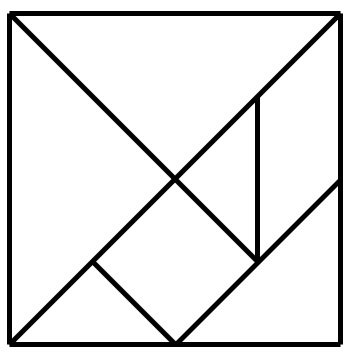
- Laat bij de driehoeken ook de indeling volgens de hoeken en de zijden geven (bv. rechthoekige, gelijkbenige driehoek).
- Vlugge werkers kan je het verband tussen de verschillende driehoeken laten zoeken (de twee kleinste driehoeken vormen samen de driehoek rechts beneden, en de grote driehoeken zijn het dubbele van de driehoek rechts beneden. De twee kleinste driehoeken vormen trouwens samen ook het vierkant of het parallellogram.)
Je knipt het toiletpapierrolletje open langs de zwarte lijn. Welke vlakke figuur krijg je als je het rolletje dan openvouwt?

- Laat dit uitvoeren tijdens de bespreking.
Welke figuur herken je in deze honingraat? Geef de best passende naam.

- Bespreek wat maakt dat geen gewone zeshoeken, maar wel regelmatige zeshoeken gebruikt worden. Doordat alle zijden en hoeken even groot zijn ‘passen’ de zeshoeken mooi aan elkaar zonder dat er gaten zitten tussenin.
- Ter info: de regelmatige zeshoek blijkt de meest interessante keuze te zijn voor de bijen. Eén cel moet voldoende groot zijn voor een bij, er mogen geen gaten tussen de cellen zijn om de plaats zo goed mogelijk te gebruiken. Bovendien maken de bijen de cellen zelf met was die ze produceren, de vorm moet dus ook zo zijn dat er zo weinig mogelijk was wordt gebruikt.
De zijvlakken van dit melkbrik hebben niet allemaal dezelfde vorm. Welke vormen zijn er? Geef telkens de best passende naam. Met de dop hoef je geen rekening te houden.

Pas de opgave aan naargelang de verpakking die je voorhanden hebt, het is belangrijk dat leerlingen kunnen checken op het echte voorwerp.
- Begin in de bespreking met de opstaande zijvlakken: twee trapezia en twee rechthoeken. De trapezia zijn even groot, de rechthoeken niet. Het vlak bovenaan is een rechthoek, het grondvlak weten we op basis van de foto niet zeker, we weten wel dat het een rechthoek is (maar misschien is het een vierkant).
- Gebruik in de bespreking de correcte terminologie: zijvlak, overstaande vlakken, ruimtefiguur,…
In het witte kader zie je een aantal veelhoeken.
Geef de best passende naam van elk van deze veelhoeken.

Tip: werk met een foto van een gevel uit de buurt.
- Vraag naar de meest nauwkeurige naam bv. rechthoekige ongelijkbenige driehoek.
- Laat als leerlingen de classificatie gezien hebben bij een figuur alle passende namen geven bv. vierhoek – trapezium – rechthoekig trapezium.
- Ter info: je ziet hier het houden skelet van een woning in Bokrijk. De wanden worden later opgevuld bv. met leem en stro.
- Hoeveel kleine gekleurde vierkantjes zijn er in totaal aan deze puzzel?
- De kubus is opgebouwd uit kleine kubusjes. Hoeveel zijn dat er in totaal?

- Laat leerlingen de oplossingswijze verwoorden aan de hand van de correcte begrippen: elk zijvlak bestaat uit 9 vierkantjes, er zijn 6 zijvlakken dus 6 x 9 = 54 vierkantjes. We tellen 3 lagen van 9 kleine kubusjes, dus in totaal zijn er 27 kleine kubusjes.
- Koppel aan deze vraag de begrippen oppervlakte en volume: het aantal kleine vierkantjes zegt iets over de oppervlakte, het aantal kleine kubusjes zegt iets over het volume.
Jef heeft een ruit uitgeknipt in papier (geen vierkant). Hij tekent één diagonaal, en knipt de ruit dan volgens de diagonaal in twee driehoeken. Geef de meest passende naam van deze driehoeken.
Je kan een analoge opgave maken door de ruit te vervangen door een andere vierhoek, of door ‘diagonaal’ te vervangen door ‘symmetrieas’.
- Observeer leerlingen bij het werken; tekenen is hier heel belangrijk om zicht te krijgen op de opgave; het is ook goed om verschillende verdelingen en ruiten te schetsen om te zien of er verschillende mogelijkheden zijn. Expliciteer dit tijdens de bespreking.
- Oplossing: de driehoeken zijn gelijk, en ze zijn zeker gelijkbenig aangezien alle zijden van een ruit even lang zijn. Het kan een gelijkzijdige driehoek zijn. De driehoek is scherphoekig of stomphoekig, dat kunnen we niet zeker weten. Het kan geen rechthoekige driehoek zijn, want in de opgave staat dat het niet om een vierkant gaat.
Zijn de diagonalen van een rechthoek ook symmetrieassen van deze rechthoek?
Je kan een analoge opgave maken door de rechthoek te vervangen door een andere vierhoek.
- Observeer leerlingen bij het werken, een schets maken is hier een meerwaarde, leerlingen kunnen zich het probleem ook proberen voorstellen met een rechthoek die ze bij de hand hebben (bv. een blad papier). Expliciteer de heuristieken ‘werken met een tekening’, ‘je het probleem proberen voorstellen’ in de nabespreking.
- Besteed in de nabespreking aandacht aan de verwoording van het begrip ‘symmetrie’, probeer zeker uit door de rechthoek te laten vouwen op een diagonaal.
- Daag vlugge werkers uit met de vraag of ze vierhoeken kennen waar de diagonalen wel symmetrieassen zijn. Als de classificatie van vierhoeken gekend is kan je ook vragen of de conclusie voor alle rechthoeken geldt (vierkanten zijn ook rechthoeken en bij een vierkant is een diagonaal wel symmetrieas).