Wiskundetaal
Lengte, afstand, breedte, hoogte, omtrek, meter, decimeter, centimeter, millimeter, kilometer, eenheid
Eindtermen
ET 2.1 De leerlingen kennen de belangrijkste grootheden en maateenheden met betrekking tot lengte, oppervlakte, inhoud, gewicht(massa) tijd, snelheid, temperatuur en hoekgrootte en ze kunnen daarbij de relatie leggen tussen de grootheid en de maateenheid.
ET 2.2 De leerlingen kennen de symbolen, notatiewijzen en conventies bij de gebruikelijke maateenheden en kunnen meetresultaten op veelzijdige wijze noteren en op verschillende wijze groeperen.
ET 2.3 De leerlingen kunnen veel voorkomende maten in verband brengen met betekenisvolle situaties.
ET 2.6 De leerlingen kunnen allerlei verbanden, patronen en structuren tussen en met grootheden en maatgetallen inzien en ze kunnen betekenisvolle herleidingen uitvoeren.
ET 2.7 De leerlingen kunnen met de gebruikelijke maateenheden betekenisvolle herleidingen uitvoeren.
ET 2.8 De leerlingen kunnen schatten met behulp van referentiepunten.
ET 2.9 De leerlingen kunnen op een concrete wijze aangeven hoe ze de oppervlakte en de omtrek van een willekeurige, vlakke figuur en van een veelhoek kunnen bepalen.
Basis
- Werk rond referentiematen: laat leerlingen de lengte van een voorwerp schatten op basis van een referentiemaat (bv. schat de lengte van de klas), of laat de juiste eenheid bij een maatgetal invullen (bv. mijn handspan is 15 …).
- Geef eenvoudige schatoefeningen (bv. toon 1 meter met je handen, bv. leg twee potloden 10 cm uit elkaar, schat je handspan) en laat controleren.
- Laat lijnstukken met een bepaalde lengte tekenen.
- Werk rond basisherleidingen met de gekende eenheden voor lengte.
- Geef opdrachten waarbij leerlingen moeten herleiden om de maten te vergelijken (bv. duid aan wat meer is dan 1 m: 45 cm – 110 cm – 200 mm; bv. orden van klein naar groot: 145 cm – 1,02 m – 300 mm; bv. hoeveel stukken van 60 cm kan ik halen uit een touw van 3 m).
- Combineer de herleidingsopgaven ook met breuken (bv. ½ m = … cm).
- Combineer de herleidingsopgaven met referentiematen door de komma op de juiste plaats te laten zetten (bv. plaats de komma zodat het klopt: het potlood is 120 dm lang).
- Laat de omtrek van een figuur berekenen. Neem zowel ‘gekende veelhoeken’ waarbij leerlingen eigenschappen van de figuur gebruiken om handig te werken (bv. rechthoek, regelmatige zeshoek) als grilligere figuren. In de derde graad komt hier ook de omtrek van een cirkel bij. Besteed aandacht aan de notatie van de eenheden.
- Laat vanuit de omtrek een bepaalde afmeting bepalen (bv. vanuit de omtrek en de lengte van een rechthoek de breedte berekenen).
- Laat leerlingen zelf contexten bedenken bij het begrip omtrek (bv. lengte omheining), gebruik het begrip in combinatie met ‘oppervlakte’ om het verschil uit te klaren.
- Laat leerlingen een figuur met een bepaalde omtrek tekenen.
Toepassingen
Het haar van een mens groeit ongeveer 0,3 mm per dag. Hoeveel centimeter is dat ongeveer per jaar?
- Ga in op de gekozen rekenwijze: hebben leerlingen dit geschat of precies berekend? Is het nodig om te weten of het om een schrikkeljaar gaat of niet? Enkele mogelijkheden:
– Precies rekenen: 365 x 0,3 mm = (365 x 3 mm):10 = 109,5 mm > afgerond 110 mm of 11 cm.
– Schattend rekenen: 400 x 0,3 mm = 120 mm = 12 cm (ongeveer 1 cm per maand)
- Laat leerlingen tonen hoe lang dit ongeveer is, en laat hen dit checken op een lat.
Als je een rondje rond onze speelplaats loopt heb je 160 meter gelopen. Hoeveel rondjes moet je lopen om 1 km af te leggen?
Tip: Pas deze opgave aan jouw speelplaats of een looppiste in de buurt aan. Geef eventueel de afmetingen, zodat leerlingen zelf eerst de omtrek moeten bepalen.
- Bespreek de ‘afronding’ van het resultaat. Er wordt gevraagd naar het aantal (volledige) rondjes, dus 6 rondjes is niet voldoende om aan 1 km te geraken.
Kijk welke schoenmaat je hebt.
Vermenigvuldig dit getal met 6,6 mm.
Zet het resultaat om naar centimeter.
Dit is de lengte van jouw voet.
Controleer maar!
- Tip: Je kan deze opdracht ook voor één schoenmaat laten doen, zodat niet iedereen hoeft te controleren.
- Tip: Je kan leerlingen ook laten rekenen met een rekenmachine, zodat ze hier volledig kunnen focussen op de herleiding.
- Bespreek welke wiskundige kennis nodig was om deze opgave aan te pakken (betekenis ‘vermenigvuldigen’, cijferen, herleiden van mm naar cm).
- Bespreek waarom je hier voor cijferen kiest in de plaats van hoofdrekenen of schattend rekenen.
Er zijn op dit moment al 307 albums van Jommeke verschenen. Stel dat je al deze albums op een stapel legt. Hoe hoog zou deze stapel ongeveer zijn?
De foto helpt je op weg!

- Bekijk hoe de leerlingen de oplossingswijze genoteerd hebben. Een mogelijkheid is hier het werken met een pijlenschema of verhoudingstabel.
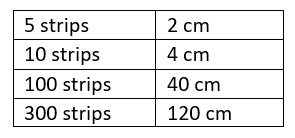
- Bespreek of leerlingen geschat hebben (op basis van 300 albums) of precies gerekend hebben.
- Laat het verkregen resultaat in meter omzetten, en laat dan leerlingen tonen hoe hoog de stapel zal zijn (ongeveer 1,2m) – gebruik de eigen lengte als referentiemaat.
Volgens de verpakking zitten 160 velletjes op deze keukenrol. Eén vel heeft afmetingen 11 cm x 23 cm.
Als ik de rol helemaal uitrol, hoeveel meter keukenpapier heb ik dan?

- Laat verwoorden wat de notatie ’11 cm x 23 cm’ betekent. Laat leerlingen aan de hand van een keukenrol en de afbeelding uitleggen waarom ze moeten rekenen met ’11 cm’ en niet met ’23 cm’.
- Besteed aandacht aan de manier waarop leerlingen deze bewerking uitgerekend hebben en aan de correcte notatie van de oplossingswijze.
- Laat het resultaat eventueel afronden tot op 1 meter.
- Leg de link met referentiematen, kunnen leerlingen zich de afmeting 18 m voorstellen?
Oom Dagobert legt 1 miljoen euro in briefjes van 200 euro naast elkaar (met de korte zijde tegen elkaar). Hoe lang is de rij briefjes ongeveer?

- Bespreek met de leerlingen hoe ze stapsgewijs kunnen werken
5 biljetten is 1000 euro, dus 5000 biljetten is 1 miljoen euro
1 biljet is ongeveer 15 cm lang
5000 x 15 cm = 75000 cm = 750 m
- Vergelijk deze lengte met een afstand die herkenbaar is voor de leerlingen.
- Laat leerlingen verwoorden welke wiskundige kennis en vaardigheden ze nodig hadden voor deze opgave (grote getallen, lengtematen herleiden)
Tiebe en Wout poseren in mini-Europa voor de Eiffeltoren. Tiebe is de oudste en is 162 cm lang.
Hoe hoog is de Eiffeltoren in mini-Europa ongeveer?

Tip: Je kan deze opgave aanpassen met een foto van een standbeeld, gebouw uit de buurt, hoogte speeltoren op de speelplaats,…
- Bespreek met de leerlingen welke gegevens nodig zijn: de lengte van de jongen en een schatting van het aantal keer dat deze lengte in de lengte van de toren past (verhouding).
- Bespreek de werkwijze: de lengte van Tiebe gaat ongeveer 7 à 8 keer in de lengte van de toren. Op die manier kom je aan ongeveer 11 tot 13 meter voor de hoogte van de toren.
- Ga in op wat een zinvolle eenheid voor de hoogte van de toren is.
- Ga in op de rekenwijze: hebben leerlingen precies gerekend of gewerkt met een schatting? Aangezien de verhouding niet precies kan bepaald worden op de figuur is het werken met een schatting hier zeker aangewezen.
- Bespreek welke wiskundige kennis nodig was om deze opgave aan te pakken (verhouding schatten, ongeveer rekenen, herleiden).
- Tip: als leerlingen ‘schaalbegrip’ al gezien hebben kan je meegeven dat de schaal van de gebouwen in mini-Europa 1/25 is. Laat sterke rekenaars op basis hiervan de hoogte van de echte Eiffeltoren bepalen, en check met de realiteit.
- Ter info: de echte Eiffeltoren is 317 m tot aan de top van de vlaggenstok, en 324 m inclusief de antenne. Aangezien het metaal krimpt of uitzet met de temperatuur kan de hoogte van de toren tot 15 cm verschillen afhankelijk van het weer!
De afmetingen van dit speeltuintje zijn 12 m x 20 m. Voor de omheining betaalt de gemeente 13 euro per meter.
Hoeveel kost de totale omheining van dit speeltuintje?

Tip: Je kan deze opgave aanpassen aan de context: gebruik de afmetingen van de speelplaats, een parkje in de buurt, de klas. Werk met omheiningen, plantenborders, plinten,… Je kan ook enkel de lengte van de omheining laten bepalen.
- Laat leerlingen bij elkaar kijken hoe ze genoteerd hebben – wie heeft een schets gemaakt?
- Laat leerlingen bij het verwoorden van de werkwijze gebruik maken van het begrip ‘omtrek’.
- Tip: je kan de opgave complexer maken door bv. te laten berekenen hoeveel rollen omheining nodig zijn, als je weet dat de omheining op rollen van 5 meter verkocht wordt.
De wielen van de fiets van Wout hebben een diameter van 60 cm.
Hoeveel meter heeft de fiets afgelegd als de wielen 100 keer rondgedraaid zijn?

- Laat leerlingen verwoorden dat ze hiervoor de formule voor omtrek van een cirkel nodig hebben.
- Bepaal vooraf of je wil dat leerlingen hier cijferen of rekenen met het rekentoestel.
- Laat het resultaat eventueel uitdrukken in km.
- Ga eventueel in op het feit dat de diameter van wielen vaak in inch gegeven wordt. Voor kinderen met een lengte tussen 140 cm en 160 cm raadt men een diameter van 24 inch aan. (1 inch = 2,54 cm)
- Tip: Sterke rekenaars kan je uitdagen met de omgekeerde opgave: Hoeveel rondjes moet het wiel draaien om een afstand van 1 km afgelegd te hebben?