Wiskundetaal
Deel, geheel, procent, percent, verhouding
Eindtermen
ET 1.3 De leerlingen kennen de betekenis van: optellen, aftrekken, vermenigvuldigen, delen, veelvoud, deler, gemeenschappelijke deler, grootste gemeenschappelijke deler, kleinste gemeenschappelijk veelvoud, procent, som, verschil, product, quotiënt en rest. Zij kunnen correcte voorbeelden geven en kunnen verwoorden in welke situatie ze dit handig kunnen gebruiken.
ET 1.5 De leerlingen kunnen natuurlijke getallen van maximaal 10 cijfers en kommagetallen (met 3 decimalen), eenvoudige breuken, eenvoudige procenten lezen, noteren, ordenen en op een getallenlijn plaatsen.
ET 1.6 De leerlingen kunnen volgende symbolen benoemen, noteren en hanteren: = ≠ < >+ – x . : / ÷ % en ( ) in bewerkingen.
ET 1.18 De leerlingen kunnen in eenvoudige getallen de gelijkwaardigheid tussen kommagetallen, breuken en procenten vaststellen en verduidelijken door omzettingen.
ET 1.15 De leerlingen kunnen eenvoudige procentberekeningen maken met betrekking tot praktische situaties.
Basis
- Geef opgaven over de relatie tussen breuk, procent en kommagetal (bv. 70/80 = …%, bv. orden de getallen 60%, 3/4 en 0,7). Besteed hierbij voldoende aandacht aan de veel gebruikte percentages.
- Geef opgaven over het nemen van een procent van een getal (bv. 20% van 150 is ..), besteed ook hier vooral aandacht aan eenvoudige percentages.
- Geef opgaven waarbij leerlingen het procent moeten bepalen (bv. Je behaalt 32 op 40 op een toets, hoeveel procent is dat?)
- Geef opgaven waarbij leerlingen het geheel moeten bepalen (bv. 30 is 20% van..)
- Geef opgaven waar procenten gebruikt worden om een toename of een afname aan te geven (bv. Je krijgt 10% korting op een kledingstuk van 36 euro. Hoeveel kost dit stuk nog?), gebruik hierbij ook expliciet de woorden korting, stijging, toename, afname in de opgave.
Toepassingen
Een paard mag ongeveer 15% van zijn lichaamsgewicht dragen. Hoeveel mag een ruiter op een paard van 600 kg maximaal wegen?
- Ter info: het paard kan iets meer dragen (tot 20% van zijn gewicht), maar aangezien het gewicht van de uitrusting er nog bovenop komt gebruikt men meestal de limiet 15 à 17% voor de ruiter.
- Je kan bij de bespreking van deze opgave ook de link leggen met het gewicht dat een mens kan dragen. Het gewicht van een boekentas mag maximaal 10% van het lichaamsgewicht bedragen – laat leerlingen berekenen en checken.
De Afrikaanse olifant is met uitsterven bedreigd. 100 jaar geleden waren er 5 miljoen van deze olifanten.
Nu zijn ze nog met ongeveer 400 000. Dat is ...% van het aantal Afrikaanse olifanten een eeuw geleden.

- Laat leerlingen hun werkwijze uitleggen, besteed aandacht aan het zoeken van het percent (deel t.o.v. geheel) en het zoeken naar een bruikbare gelijkwaardige breuk (bv. 400 000 / 5 000 000 = 4 / 50 = 8/100 = 8%)
- Laat het resultaat controleren via een schatting, bv. door het aantal olifanten af te ronden op 500 000 komen we aan een deel van 1/10 = 10%.
- Vraag ook met hoeveel percent het aantal olifanten gedaald is op 100 jaar.
- Laat leerlingen verwoorden welke wiskundige kennis en vaardigheden ze nodig hadden bij deze opgave (betekenis percent, breuken vereenvoudigen, een breuk omzetten naar een percent, weten hoeveel 1 miljoen is).
- Duid het uitsterven van de Afrikaanse olifant: het dier heeft minder leefruimte, en is ook erg bedreigd door ivoorstropers.
Apestaartjaren is een grote tweejaarlijkse bevraging over het mediagebruik van kinderen en jongeren. Hieronder zie je de antwoorden op de vraag: ‘Hoe vaak game je gemiddeld per dag?’
Ongeveer 1000 kinderen en jongeren gaven aan dat ze op een schooldag tussen 1 en 3 uur per dag gamen. Hoeveel kinderen en jongeren werden in dit onderzoek bevraagd?
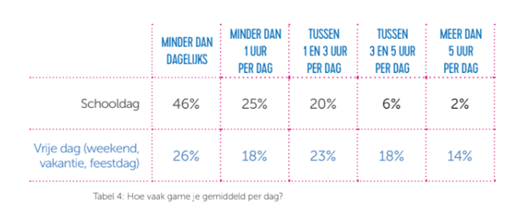
- Bekijk tijdens de bespreking samen de tabel. Laat opmerken/uitleggen dat de som van de percentages op één rij niet 100 is (wellicht door afrondingen).
- Laat de 20% die nodig is voor het oplossen van de vraag eventueel vervangen door ‘1/5’, hierdoor wordt de oplossingsmethode duidelijker.
- Opmerking: de onderzochte groep bestond uit 1000 kinderen tot 12 jaar en 4000 jongeren boven de 12, de gegevens zijn dus wellicht niet volledig herkenbaar. Je kan wel aftoetsen hoe de verdeling er in jullie klas zou uitzien, en dit omzetten naar procenten.
- Tip: op de website ‘Apestaartjaren.be’ vind je meer cijfers.
Welk bedrag staat onder de vlek? Je mag ongeveer rekenen.

Deze opgave kan je makkelijk aanpassen naar een koopje dat binnen de interessesfeer van de klas ligt. Het is interessant om het gegeven ‘korting’ te combineren met schattend rekenen aangezien het meestal volstaat een idee te hebben van hoe groot de korting is.
- Besteed in de bespreking aandacht aan de afronding van de prijs en aan de rekenwijze.
- Laat leerlingen verwoorden waarom prijzen vaak op 99 cent eindigen.
Ons lichaam telt in het totaal 206 botten. In je voeten zitten heel veel kleine botjes: in elke voet zitten 26 botten! Hoeveel procent van de botten in je lichaam zit in je voeten? Je mag ongeveer rekenen.
- Bespreek de benaderingen die leerlingen maakten. De breuk 52/206 kan je best benaderen door 1/4 of 25%.
- Ter info: een voet bevat zoveel botten omdat het lopen en allerlei verschillende bewegingen die je met de voet doet (zoals ook springen, klimmen,…) soepel zou kunnen gebeuren.
Bekijk de grafiek. Schrijf wat je kan aflezen in 4 zinnen, maar gebruik eenvoudige breuken in de plaats van procenten.

- Laat werken met eenvoudige breuken: 1/2, 2/5, 3/10, 1/4.
- Laat leerlingen verwoorden hoe het komt dat de som van deze percentages meer is dan 100%.
- Laat leerlingen uitleggen hoe de hoogtes van de rode rechthoeken in de grafiek bepaald worden. Hoe kun je (ongeveer) zien dat de verhoudingen kloppen?
Het glazen potje yoghurt werd op de weegschaal gezet. Kijk goed naar de getallen op de foto’s.
Vul aan: ‘De verpakking is ……% van het totale gewicht van het potje.’
Je mag met afgeronde getallen rekenen.

Deze opgave kan je makkelijk aanpassen met andere verpakkingen.
- Laat leerlingen de gegevens verwoorden aan de hand van de begrippen ‘bruto, netto, tarra’.
- Besteed in de bespreking aandacht aan de afronding (je kan 265 gram benaderen door 250 gram om handig te rekenen).
- Laat de verschillende manieren om de breuk 100/250 als een percent te schrijven verwoorden (bv. door te vereenvoudigen naar de breuk 2/5 = 40%, of door te herleiden naar de breuk 400/1000 = 40%).
In een kledingzaak staat bij een stapel T-shirts deze promotie:
‘Tweede T-shirt aan de helft van de prijs!’
Je koopt twee van deze T-shirts. Hoeveel procent korting krijg je eigenlijk?
- Maak bij de bespreking de opgave concreter door met voorbeelden te werken. Stel dat één T-shirt 20 euro kost, hoeveel betaal je dan voor de beide T-shirts? (30 euro) En hoeveel zou je betalen mocht er geen promotie zijn? (40 euro). Hoeveel korting krijg je? (10 euro korting op 40 euro) Hoeveel procent is dat? (25%)
- Expliciteer de heuristiek die hier bruikbaar is: ‘met eenvoudige voorbeelden werken’.