Wiskundetaal
Recht evenredig, omgekeerd evenredig, verhouding
afstand-snelheid-tijd, gemiddelde snelheid, schaal, prijs-hoeveelheid
Eindtermen
ET 1.21 De leerlingen zijn in staat in concrete situaties (onder meer tussen grootheden) eenvoudige verhoudingen vast te stellen, te vergelijken, hun gelijkwaardigheid te beoordelen en het ontbrekend verhoudingsgetal te berekenen.
Basis
Het vaststellen van een (recht) evenredig verband tussen grootheden zal zich meestal in contexten situeren: relatie prijs en aangekochte hoeveelheid, relatie aantal personen en hoeveelheid ingrediënten in recepten, relatie afstand/tijd bij snelheid, relatie afstand op de figuur en afstand in werkelijkheid bij schaal,… Belangrijk is dat leerlingen er bewust bij stilstaan dat er effectief een recht evenredig verband is (en ze dus een verhoudingstabel of pijlenschema mogen gebruiken) in die context; niet elk verband is immers een recht evenredig verband; zelfs niet altijd in de genoemde contexten (bv. bij een promoactie als ‘2 kopen 3e gratis’ geldt dit verband niet).
Toepassingen
Op elk voedingsmiddel staat de energiewaarde vermeld, uitgedrukt in kcal (kilocalorie).
Een blikje cola geeft je 140 kcal. Hoe lang moet je wandelen om deze energie te verbruiken, als je weet dat je per half uur wandelen 120 kcal verbruikt?
Tip: pas deze opgave aan, werk met een ander voedingsmiddel (breng eventueel de verpakking mee om de calorieën af te lezen) en met een andere activiteit (bv. fietsen).
- Laat leerlingen met elkaar vergelijken hoe ze de oplossingswijze noteerden. Welke voorstelling (bv. pijlenschema, verhoudingstabel) gebruikten ze?
- Voorbeeld oplossing via verhoudingstabel:

- Bespreek waarom deze rekenwijze hier kan – het calorieverbruik is recht evenredig met de tijd van de activiteit, daarom kan je werken met de verhoudingstabel/het pijlenschema.
- Vergelijk de verschillende manieren van rekenen – op welke manier kan dit efficiënt?
Het vrijheidsbeeld in New York is 90 meter hoog.
Er bestaat ook een lego-bouwdoos van het vrijheidsbeeld.
De hoogte van het vrijheidsbeeld in lego is 45 cm.
Wat is de breukschaal van dit model?

Je kan deze context aanpassen, werk met een ander schaalmodel van een wagen of gebouw, een afbeelding van een dier,…
- Laat het schaalbegrip verwoorden.
- Werk met een schema om de schaal te vinden, bv. verhoudingstabel.
Een jachtluipaard loopt In volle sprint 30 meter per seconde.
Hoeveel bedraagt zijn topsnelheid uitgedrukt in km/h?

Gelijkaardige oefeningen kan je maken met andere ‘snelle’ of ‘trage’ dieren.
- Benadruk in de bespreking de oplossingsmethode bij opdrachten rond snelheid (bv. verhoudingstabel of pijlenschema).
- Vergelijk deze snelheid met de maximaal toegelaten snelheid op bv. een autosnelweg. Benadruk dat het om ‘topsnelheid’ gaat, en dus niet om ‘gemiddelde snelheid’.
- De cheeta is het zich snelst voortbewegende landdier.
Bekijk dit infobord. Met welke gemiddelde wandelsnelheid heeft men hier gerekend?

Tip: werk met een afstand uit de schoolcontext (bv. laat leerlingen jouw gemiddelde snelheid bij het parcours school-thuis berekenen)
- Leerlingen kunnen eerst een schatting maken, of na het maken van de opdracht nagaan of het resultaat realistisch is. Bespreek ook enkele ‘referentiesnelheden’ (bv. wandelsnelheid, fietssnelheid, snelheid auto in de straat van de school, op de autosnelweg)
- Benadruk in de bespreking de oplossingsmethode bij opdrachten rond snelheid (bv. verhoudingstabel of pijlenschema).
Op de foto zie je de snelheidsbeperking op de Nederlandse snelwegen.
Sjoerd rijdt rond 20u ‘s avonds aan de maximale snelheid gedurende 20 minuten van Dordrecht naar Breda. De volgende middag doet hij hetzelfde traject terug, opnieuw aan de maximum snelheid.
Hij is nu … minuten langer/minder lang onderweg dan de vorige avond.

- Een mogelijkheid is om eerst de afstand (40 km) te berekenen, en dan de nodige tijd om deze afstand aan 100 km/h af te leggen. Besteed aandacht aan het stapsgewijs noteren van deze redenering.
- Mogelijk hebben sommige leerlingen ook gewerkt met de omgekeerd evenredigheid tussen snelheid en tijd in deze situatie.
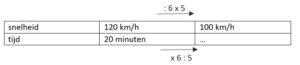
- Vraag naar de maximum snelheid op Belgische snelwegen. Ga eventueel in op de keuze van de Nederlandse overheid om de snelheid te verlagen (voornamelijk milieuredenen, bij een lagere snelheid is het brandstofverbruik, en dus ook de uitstoot lager).
- Besteed aandacht aan de heuristiek ‘het probleem opsplitsen in deelproblemen’.
Bij een zebrapad zijn de witte strepen altijd 50 cm breed, en is de afstand tussen de strepen ook steeds 50 cm.
Op dit kruispunt is het 20 seconden groen licht voor voetgangers.
Met welke snelheid moet je dit kruispunt oversteken om zeker op tijd aan de overkant te zijn?

Pas de context aan met een verkeerslicht in de buurt van de school. Je kan eventueel ook gewoon de breedte van de straat geven in de plaats van te werken met de strepen van het zebrapad.
- Laat leerlingen verwoorden welke zaken ze nodig hebben om de snelheid te kunnen bepalen: breedte van de straat en tijd. De afstand kan je hier niet precies bepalen op basis van de foto, je kan werken met een benadering van 7 meter.
- Laat leerlingen vergelijken hoe ze stapsgewijs gewerkt hebben om te komen tot de snelheid in km per uur.
- Vergelijk deze snelheid met de gemiddelde wandelsnelheid.