Wiskundetaal
Breuk, teller, noemer, geheel, deel, breukstreep, deling, “… van de … gelijke delen van het geheel”, gelijkwaardig breuken, breuken vereenvoudigen, onvereenvoudigbaar
Eindtermen
ET 1.4 De leerlingen herkennen in voorbeelden dat breuken kunnen uitgelegd worden als: een stuk (deel) van, een verhouding, een verdeling, een deling, een vermenigvuldigingsfactor (operator), een getal (met een plaats op een getallenlijn), weergave van een kans. De leerlingen kunnen volgende terminologie hanteren: stambreuk, teller, noemer, breukstreep, gelijknamig, gelijkwaardig.
ET 1.5 De leerlingen kunnen natuurlijke getallen van maximaal 10 cijfers en kommagetallen (met 3 decimalen), eenvoudige breuken, eenvoudige procenten lezen, noteren, ordenen en op een getallenlijn plaatsen.
ET 1.22 De leerlingen kunnen eenvoudige breuken gelijknamig maken in functie van het optellen en aftrekken van breuken of in functie van het ordenen en het vergelijken van breuken.
Basis
- Geef opgaven waarbij leerlingen een bepaald deel van een figuur moeten inkleuren.
Geef opgaven waarbij leerlingen aangeven welk deel van een figuur gekleurd is / wit is. Breng variatie in de vorm van het geheel en het aantal delen waarin het geheel verdeeld is, en zorg zowel voor figuren als aantallen die verdeeld zijn.
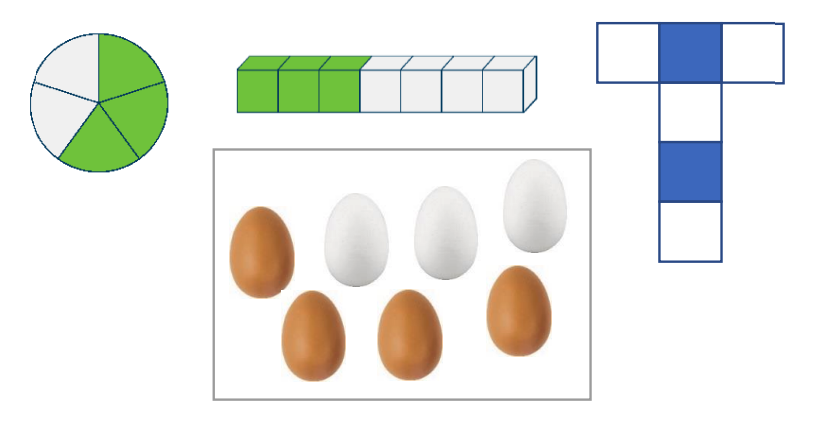
- Geef opgaven waarbij leerlingen een breuk moeten herstructureren bv.
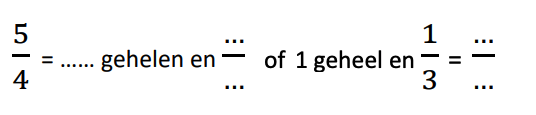
- Geef een breuk en laat leerlingen gelijkwaardige breuken zoeken (bv. geef 3 breuken die gelijkwaardig zijn met de breuk 2/6); of laat leerlingen de breuken die gelijkwaardig zijn met een gegeven breuk zoeken in een reeks breuken (bv. omcirkel alle breuken die gelijkwaardig zijn met de breuk 2/6).
- Laat een gegeven breuk zo ver mogelijk vereenvoudigen.
- Geef een getallenas waarop leerlingen een gegeven breuk moeten plaatsen (bv. de breuk 2/5 op een getallenas waar het geheel in 10 verdeeld is).
Toepassingen
In de tabel zie je hoe de kinderen van klas 4A naar school komen. Welk deel van de leerlingen komt te voet naar school?

Pas de gegevens aan je klascontext aan. Je kan ook werken met bv. lievelingskleur, seizoen waarin leerlingen jarig zijn, aantal jongens/meisjes in de klas,…
- Laat leerlingen de gegevens eventueel ook voorstellen in een staafdiagram.
Papa, Saar en Bent verdelen de ruimte in de boekenkast. Welk deel van de boekenkast mag Bent vullen?

- Vestig indien nodig aandacht op veel gemaakte fout: Bent heeft 4 van de 8 delen – waarom klopt dit niet? (bij breuken gaat het steeds om gelijke delen)
- Gebruik de vaste verwoording van breuken om dit op te lossen: Hoeveel gelijke delen zijn er? Hoeveel delen daarvan zijn er voor Bent?
- Besteed aandacht aan de manier waarop leerlingen de oplossingswijze kunnen duidelijk maken op de figuur (onderverdelen in 10 gelijke delen, aantal delen Bent arceren).
De strook stelt de wereldbevolking voor. Dat zijn meer dan 7 miljard mensen.
12/20 van de bevolking woont in Azië. Kleur dat deel groen.
3/20 van de bevolking woont in Afrika. Kleur dat deel geel.
3/20 van de bevolking woont in Amerika. Kleur dat deel rood.
2/20 van de bevolking woont in Europa. Kleur dat deel bruin.
Duid ook de gebruikte kleuren aan.
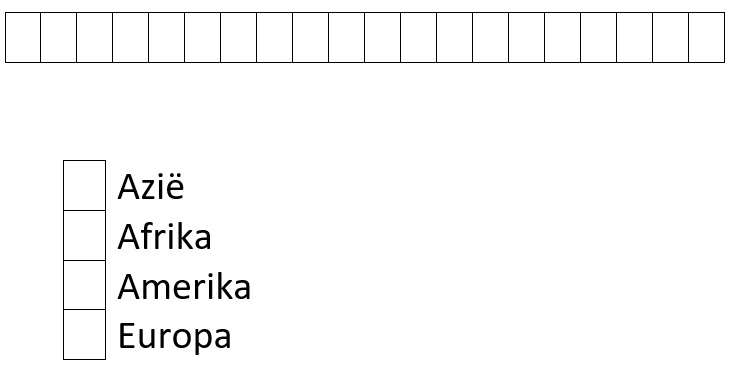
- Leerlingen merken misschien op dat een continent ontbreekt in de opsomming (Oceanië). In Oceanië woont ongeveer 1/200 van de wereldbevolking. De strook zou dus fijner moeten verdeeld zijn om dit weer te geven. Ook de andere gegevens zijn afgerond, de figuur is dus een grove benadering. Noord- en Zuid-Amerika werden hier ook samengenomen voor de eenvoud van de voorstelling.
- Bespreek met de leerlingen welke voorstelling het meest overzichtelijk is: de lijst met breuken of de weergave in de strook.
- Gebruik het woord ‘legende’ in de bespreking.
In 75 van de ongeveer 200 landen op de wereld is de regel dat je links van de weg moet rijden.
In welk deel van de landen rijdt men links?
Vereenvoudig de breuk zo ver mogelijk.
- Bespreek met de leerlingen ook het nut van de vereenvoudigde breuk: 3/8 is duidelijker dan 75/200.
- Ter info: gebieden waar men links rijdt zijn naast het Verenigd Koninkrijk o.a. oud-Britse kolonies zoals Zuid-Afrika en Australië.
- Het links rijden stamt naar het schijnt van de periode waarin mensen zich te paard verplaatsten. Aangezien de meeste mensen rechtshandig zijn, en dus ook hun zwaard rechts dragen, was het makkelijker om je te verdedigen met een zwaard als je links van de weg reed.
Pieter neemt de helft van 1/4 van een taart. Welk deel van de taart neemt Pieter?
Opmerking: Deze opgave staat hier als inoefening van breukbegrip, dus voordat leerlingen hebben leren breuken delen.
- Oplossing: 1/8
- Ga in op de manier waarop je de oplossing best kan duidelijk maken. Op een figuur waarop je eerst het geheel, dan een kwart en dan de helft ervan aanduidt kan je 1/8 snel aflezen. Sommige leerlingen lossen deze opgave wellicht uit het hoofd op, daag hen uit om de oplossing te noteren zodat anderen ook begrijpen waarom dit klopt.
- Daag sterke rekenaars uit met analoge opgaven (bv. de helft van 1/3, de helft van 1/5) – misschien vinden ze een regelmaat?
- Besteed aandacht aan de heuristiek ‘een tekening maken’.
Welk deel van de benzinetank is gevuld?

Pas eventueel aan, gebruik bv. de batterij-aanduiding van smartphone of laptop.
- Het geheel is hier geen volledige cirkel, dit kan mogelijk verwarrend zijn voor leerlingen. Het is wel belangrijk dat leerlingen weten dat ‘het geheel’ er op verschillende manieren kan uitzien.
- Werk bij het bespreken van deze opgave gericht vanuit de betekenis van teller en noemer. “Wat is het geheel?” (de volledige inhoud van de tank, het boogje) / “Wat vertelt de noemer?” (in hoeveel gelijke delen het geheel verdeeld is) / “In hoeveel delen is het geheel verdeeld?” (in 4 x 3, dus in 12 deeltjes) / “Wat vertelt de teller?” (hoeveel deeltjes nog zichtbaar zijn
In de figuur hieronder zie je een ‘tangram’.
Dat is een oude Chinese puzzel die bestaat uit 7 stukken.
Je kan er heel veel figuren mee maken.
Welk deel van de tangram is grijs gekleurd?
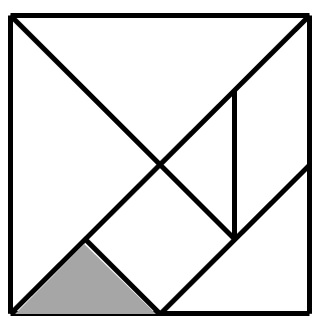
Oplossing: 1/16
Werk systematisch naar de oplossing toe:
- Over welke twee zaken moeten we iets weten als we een breuk willen schrijven?
- Wat weten we al? (het aantal grijze deeltjes)
- Wat moeten we nog weten? (in hoeveel van die driehoekjes het geheel verdeeld kan worden)
- Op welke manier kunnen we de volledige figuur verdelen in kleine driehoekjes?
- Handig: de grote driehoeken moet je eigenlijk niet verder verdelen, eens je weet dat de helft van het vierkant uit 8 driehoekjes bestaat.
- Besteed aandacht aan de heuristiek: ‘Werk op de tekening’.
De keukenvloer bestaat uit witte en blauwe tegels.
Welk deel van de tegels is blauw?
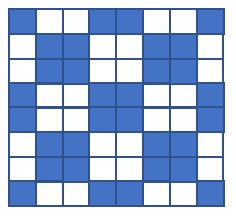
Oplossing: ½
Besteed aandacht aan verschillende oplossingsmethodes:
- Je kan alle tegels tellen (8×8), en dan tellen hoeveel blauwe tegels er zijn. Dit is wel veel werk..
- Op elke rij zijn er evenveel blauwe tegels als witte tegels. Er zijn dus in totaal evenveel blauwe tegels als witte tegels, de helft van de tegels is dus blauw.
- Misschien ontdekken leerlingen een patroon in de vloer: de vloer bestaat uit een aantal keer het patroon hieronder. In dit patroon zie je dat er evenveel blauwe als witte tegels zijn.
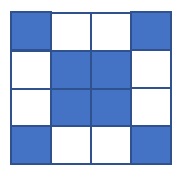
- Besteed aandacht aan de heuristiek: ‘Voor ik begin te rekenen kijk ik eerst of het makkelijker kan. Een patroon zoeken in de figuur kan helpen.’
In Breukenland zijn de huisnummers geen gewone getallen, maar breuken. Op de figuur zie je de huizen met huisnummer ‘1/6’ en huisnummer ‘1/2’.
Welk huisnummer heeft het huis juist midden tussen deze twee huizen?
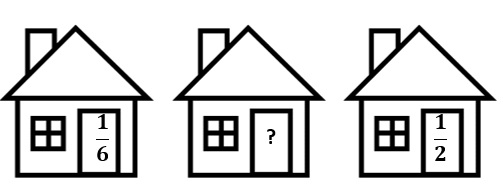
- Oplossing: 2/6 (1/3)
- Misschien hebben sommige leerlingen intuïtief 1/4 geantwoord – stel eventueel via breukenschijven voor om te laten zien dat dit niet klopt. Om het juiste antwoord te vinden kan je de breuken eventueel laten voorstellen op de getallenas, zo zien de leerlingen dat ze het geheel in 6 delen moeten verdelen. Of je kan onmiddellijk werken met gelijkwaardige breuken, door te vragen waarom het moeilijk is om te zien welke breuk in het midden ligt (omdat de noemers niet gelijk zijn).
- Besteed (indien je werkt met een getallenas) aandacht aan de heuristiek ‘De situatie proberen voorstellen’.