Getallen: Rekenen met kommagetallen

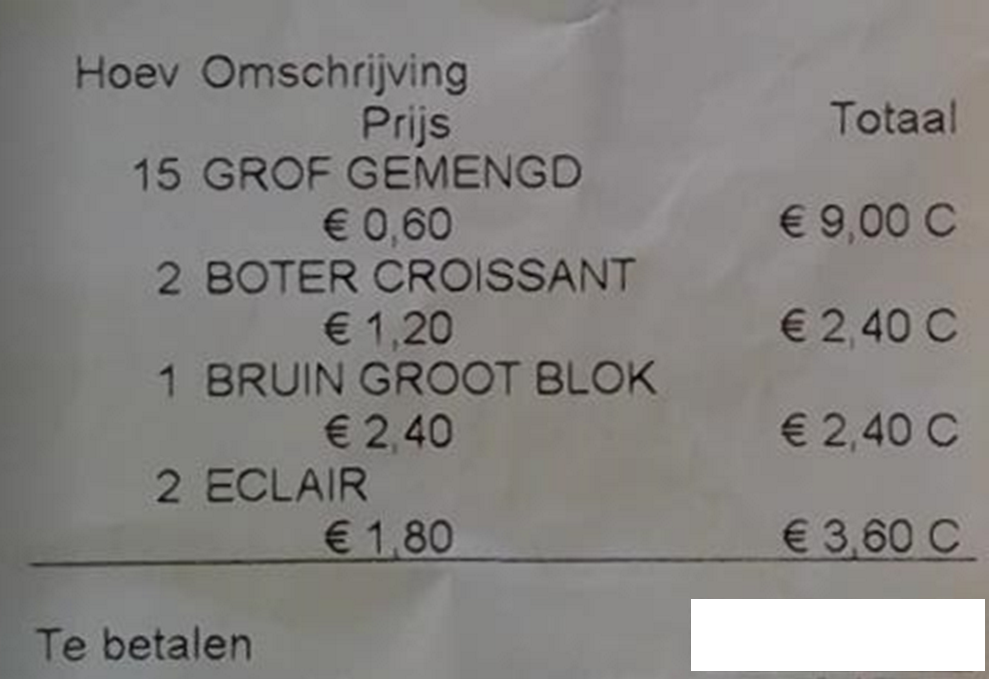
Pas de context eventueel aan: werk met een authentiek kasticket.

• Bespreek: Wat heb ik gekocht? Wat vertellen de getallen op het ticket? Welke getallen hebben we nodig?
• Bespreek of cijferen of hoofdrekenen hier het meest aangewezen is. De getallen zijn hier eenvoudig, bespreek op welke manier leerlingen de getallen samengenomen hebben om handig te rekenen.
• Ga in op referentiepunten voor prijzen bij bakker (bv. de prijs van een brood).

Pas de context aan: werk met een kaart van een zaak in de buurt, of met de kaart die gebruikt wordt op het schoolfeest, eetfestijn,…

• Bespreek het nut van dergelijke oefeningen uit het hoofd te kunnen uitrekenen: de persoon aan de kassa moet snel het te betalen bedrag kunnen zeggen.
• Laat leerlingen vergelijken op welke manier ze de gegevens en tussenstappen noteerden.
• Laat verwoorden op welke manier ze handig gerekend hebben, bv. eerst de gehele delen optellen, bv. handig samennemen.

• In het kader van referentiematen kan je deze binnentemperatuur laten vergelijken met de temperatuur in de klas. In welk seizoen kan deze buitentemperatuur voorkomen?
• Bekijk de verschillende oplossingsmethodes. Zo kunnen leerlingen werken via de aftrekking (30 – 23,8 = 30 – 23 – 0,8) maar ook via de optelling (Ik tel eerst 0,2 op bij 23,8, en dan moet ik nog 6 optellen bij 24 om aan 30 te geraken, in totaal het ik dus 6,2 opgeteld.)

• Bespreek of leerlingen voor hoofdrekenen of voor cijferen gekozen hebben.
• Bespreek op welke manier de leerlingen dit makkelijk kunnen uitrekenen. Het aanvullend optellen (0,030 bijvoegen tot 4 kg, en dan nog 0,045 kg) is hier handig.
• Als de leerlingen ‘ml’ al kennen, dan kan je erbij zeggen dat we rekenen dat 1 liter melk 1 kg weegt, we mogen dus bij benadering zeggen dat de baby 75 ml heeft gedronken.
• Gebruik referentiematen om deze hoeveelheid voor te stellen.

Pas de context eventueel aan: werk met een product dat herkenbaar is voor leerlingen uit een reclamefolder.

• Ga in op de betekenis van het woord ‘korting’.
• Ga in op de grootte van de korting: je krijgt hier ongeveer 10 euro korting op een totaalbedrag van ongeveer 40 euro – is dat veel?
• Bespreek de verschillende oplossingsmethodes: hebben leerlingen gekozen voor cijferen of hoofdrekenen en waarom? Indien ze voor hoofdrekenen gekozen hebben, welke methode hebben ze gebruikt?
• In het voorbeeld zijn er verschillende methodes:

> Cijferen: 36,95 – 27,30

> Hoofdrekenen 36,95 – 27,30 = 36,95 – 0,30 – 27

> Hoofdrekenen: 36,95 – 27,30 = (36 – 27) + (0,95 – 0,30)

> Hoofdrekenen: 36,95 – 27,30 = (37 – 27,30) – 0,05

> Hoofdrekenen via aanvullend optellen: 0,70 + 2 + 6,95

• Bespreek het afronden. (Eén mijl = 1,6 km; de wedstrijd is dus 16 km.)
• Bespreek in functie van referentiematen. Verwijs naar de referentiemaat voor 1 km. Hoe lang zou je over het traject van 10 miles doen al wandelend? (gemiddelde wandelsnelheid 5 km/h) Hoe lang zou je over dit traject doen al fietsend? (bv. aan 15 km/h) Loopsnelheid is natuurlijk relatief, je zou met een gemiddelde van 10 km/h kunnen werken.
• Bespreek welke wiskundige vaardigheden nodig zijn om deze opgave aan te pakken (1 km = 1000 m, vermenigvuldigen met 10, afronden).
• Geef achtergrondinfo. Mijl wordt als lengtemaat nog gebruikt in o.a. de Verenigde Staten en Verenigd Koninkrijk (in plaats van km).

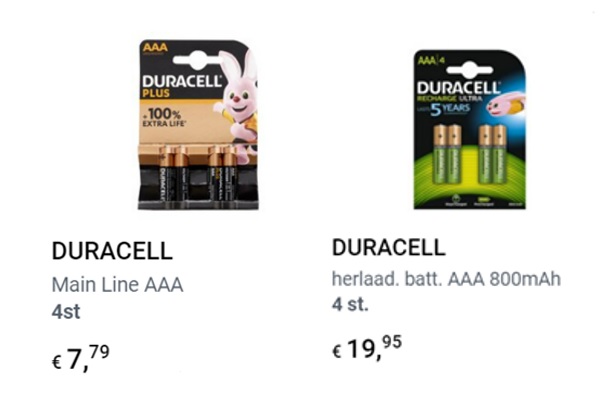
• Laat leerlingen vertellen wat ze uit de gegevens kunnen afleiden, zodat duidelijk is dat de prijs voor de 4 batterijen samen is. Toon een AAA-batterij.
• Bespreek de verschillende rekenwijzen – ga zeker in op de manier waarop leerlingen afgerond hebben.

> Het eenvoudigst is het eerste bedrag afronden naar 8 euro (2 euro per batterij) en het tweede bedrag naar 20 euro (5 euro per batterij).

> Misschien hebben leerlingen afgerond tot op een tiende. Voor de duurste soort geeft dit opnieuw 5 euro per batterij, voor de goedkoopste soort is dit 7,80 euro : 4 = 1,95 euro per batterij. Hier kan je ingaan op de berekeningswijze van 7,80 : 4 bv. (7 : 4) + (0,80 : 4) = 1,75 + 0,20 = 1,95 of (8 : 4) – (0,20 : 4) = 2 – 0,05 = 1,95

> Bespreek met de leerlingen dat de beide manieren van afronden hier hetzelfde besluit opleveren: de tweede soort is ongeveer 3 euro duurder per batterij.

• Misschien hebben leerlingen nog anders gerekend: eerst het verschil tussen de volledige verpakkingen (12,20 euro), en dit dan delen door 4. Dit geeft een exact prijsverschil.
• Ga in op het prijsverschil: de tweede soort zijn herlaadbare batterijen, die kan je veel langer gebruiken, het is dus normaal dat ze meer kosten – eigenlijk zijn ze goedkoper als je kijkt hoe vaak je ze kan gebruiken.

Tip: werk met een eigen kasticket of met een foto van een bedieningstoog waar de prijs per kg vermeld staat.

• Bekijk met de leerlingen het kassaticket: wat betekenen de getallen die erop staan? (ter info: PLU is een code voor groente en fruit die bedoeld is voor de administratie in de winkel, dit is hier niet relevant.)
• Bespreek welke bewerking we zouden maken als we exact rekenen.
• Bespreek de verschillende oplossingsmethodes en schattingen, motiveer leerlingen om met ronde getallen te werken.

bv. 336 g kaas is ongeveer 1/3 kg kaas — 14,75 euro is ongeveer 15 euro — 1/3 van 15 euro is 5 euro.

bv. 0,336 rond ik af naar 0,3 — 14,75 rond ik af naar 15 — 0,3 x 15 = (3 x 15) : 10 = 4,5

• Laat vluggerds op dezelfde manier de prijs voor de manchegokaas checken (bv. het ging om ongeveer ¼ kg kaas tegen ongeveer 28 euro per kg, dus ongeveer 7 euro voor dit stuk kaas).
• Laat leerlingen benoemen welke wiskundige vaardigheden ze nodig hadden om deze opgave aan te pakken: de prijzen op een ticket begrijpen, werken met gram en kg, kommagetallen afronden, tafels, hoofdrekenen, verband kommagetallen en breuken.
• Ga in op het nut van schatten bij het controleren van een rekening: je krijgt snel een beeld of de prijs kan kloppen.

Tip: pas de context aan op basis van een krant die jij of een leerling meebrengt. De prijs van de krant staat hierop vermeld, de prijs van een abonnement vind je op de website. Je kan ook met een magazine werken.

• Laat leerlingen de verschillende rekenwijzen voor de 300 exemplaren vergelijken. bv. 300 x 2,70 = (300 x 2) + (300 x 0,70) = 600 + 210 = 810 of bv. 300 x 2,7 = 30 x 27 = (30 x 30) – (30 x 3) = 900 – 90 = 810
• Besteed aandacht aan de notatie van de tussenstappen.
• Laat sterke rekenaars uitzoeken hoe je aan ongeveer 300 kranten per jaar komt (geen krant op zondag, en geen krant op feestdagen, dus die dagen moet je aftrekken van 365).
• Bespreek eventueel waarom een jaarabonnement niet noodzakelijk een besparing is (misschien koop je niet dagelijks de krant, als je een abonnement hebt kan je hierin niet meer kiezen).

• Laat leerlingen verwoorden wat op de afbeelding terug te vinden is en wat het verband tussen deze zaken is.
• Vergelijk de schattingen die leerlingen maakten. Een mogelijkheid is om de prijs per liter af te ronden op 1,8 euro per liter, en het aantal liter op 25 l. De berekening wordt dan 25 x 1,8 = (100 x 1,8) : 4 = 180 : 4 = 45.
• Laat ook de gebruikte hoofdrekentechniek verwoorden.
• De afbeelding zonder vlek vind je hieronder:

• Tip: in de plaats van het werken met het maanwagentje kan je ook het gewicht van een gemiddelde leerling van deze leeftijd of het gewicht van een leerkracht op de maan laten berekenen.
• Bespreek met de leerlingen of ze voor hoofdrekenen, cijferen of schattend rekenen kiezen.
• Bespreek de afronding van het product – is het zinvol dit op minder dan 1 kg nauwkeurig te weten?
• Ter info: het gewicht op de maan is kleiner omdat de aantrekkingskracht van de maan op objecten kleiner is dan de aantrekkingskracht van de aarde. Dit is zo omdat de maan zelf minder weegt dan de aarde.
• Ter info: de maanwagens zijn gemaakt voor onderzoek van de maan, op die manier kunnen ook stukken van de maan verder dan de landingsplaats onderzocht worden.

• Besteed aandacht aan stapsgewijze oplossingsmethode:

> 1l = 1000 ml, dus 1 l bevat 106 gram suiker

> 106 : 4 = (100 : 4) + (6 : 4) = 25 + 1,5 = 26,5 (hierop kan je eventueel de afrondingsregel laten toepassen.

• Daag leerlingen uit hun oplossingsmethode netjes te noteren, zodat anderen duidelijk zien welke tussenstappen ze genomen hebben.
• Laat leerlingen verwoorden welke wiskundige kennis en vaardigheden ze nodig hadden voor deze opgave (verband ml en l, handig hoofdrekenen, aflezen tabel).
• Tip: laat leerlingen op basis van voedingswaardetabel op de verpakking ook berekenen hoeveel suikerklontjes er zitten in hun favoriete soort koeken, of bv. in één brikje of blikje frisdrank.
• Sta stil bij de info uit de voedingswaardetabel.

• Oplossing: Er zijn twee mogelijkheden:

4,0 – 2,8 = 1,2

4,1 – 2,9 = 1,2

• Besteed aandacht aan hoe leerlingen weten dat ze alle mogelijkheden gevonden hebben. Misschien zie je op het zicht welke oefeningen dit kunnen zijn, maar ben je zeker dat dit de enige oplossingen zijn? Een mogelijkheid is om systematisch alle mogelijke cijfers die onder de eerste vlek kunnen zitten af te gaan: 0 en 1 zijn mogelijk, maar vanaf 2 (4,2 – 2,. = 1,2) kan de oefening niet meer kloppen.
• Besteed aandacht aan de gebruikte heuristieken. We hebben hier verschillende mogelijkheden uitgeprobeerd, op die manier hebben we gezien wat kon en wat niet kon. We zijn niet gestopt bij één mogelijkheid

• Er zijn verschillende oplossingen bv.

6 + 2 + 0,2 + 0,2 + 0,02 + 0,03

9 – 0,33 – 0,22