Wiskundetaal
Gewicht, kilo, gram, ton, weegschaal, balans, grootheid, eenheid, meten
Eindtermen
ET 2.1 De leerlingen kennen de belangrijkste grootheden en maateenheden met betrekking tot lengte, oppervlakte, inhoud, gewicht(massa) tijd, snelheid, temperatuur en hoekgrootte en ze kunnen daarbij de relatie leggen tussen de grootheid en de maateenheid.
ET 2.2 De leerlingen kennen de symbolen, notatiewijzen en conventies bij de gebruikelijke maateenheden en kunnen meetresultaten op veelzijdige wijze noteren en op verschillende wijze groeperen.
ET 2.3 De leerlingen kunnen veel voorkomende maten in verband brengen met betekenisvolle situaties.
ET 2.6 De leerlingen kunnen allerlei verbanden, patronen en structuren tussen en met grootheden en maatgetallen inzien en ze kunnen betekenisvolle herleidingen uitvoeren.
ET 2.7 De leerlingen kunnen met de gebruikelijke maateenheden betekenisvolle herleidingen uitvoeren.
ET 2.8 De leerlingen kunnen schatten met behulp van referentiepunten.
Basis
- Werk rond referentiematen: laat leerlingen het gewicht van een voorwerp schatten op basis van een referentiemaat (bv. schat het gewicht van deze appel), of laat de juiste eenheid bij een maatgetal invullen (bv. dit potje yoghurt weegt 200 …).
- Werk rond basisherleidingen met de gekende eenheden voor gewicht.
- Geef opdrachten waarbij leerlingen moeten herleiden om de maten te vergelijken ( bv. 800 g + … g = 1,5 kg; bv. hoeveel pakjes van 200 gram gaan er in 5 kg?)
- Combineer de herleidingsopgaven ook met breuken (bv. 1/5 ton = … kg).
- Combineer de herleidingsopgaven met referentiematen door de komma op de juiste plaats te laten zetten (bv. plaats de komma zodat het klopt: het gewicht van deze personenwagen is 11 ton).
- Combineer met de begrippen ‘bruto, netto, tarra’.
Toepassingen
Voor deze 4 potjes yoghurt heb ik 1,65 euro betaald.
Hoeveel kost deze yoghurt per kg?

- Laat leerlingen werkwijze verwoorden, besteed aandacht aan het verband tussen gram en kilogram.
- Laat leerlingen benoemen welke wiskundige vaardigheden ze nodig hadden om deze opgave aan te pakken (hoofdrekenen, verband g en kg).
De savanneolifant is de grootste Afrikaanse olifant. Een volwassen mannetjesdier weegt ongeveer 5 ton. Een olifantenkalfje weegt ongeveer 100 kg. Wat is de verhouding tussen het gewicht van een kalfje en een volwassen olifant?

- Als het woord ‘verhouding’ nog onvoldoende gekend is kan je de vraag aanpassen naar ‘Hoeveel keer gaat het gewicht van een kalfje in dat van een volwassen olifant?’
- Laat leerlingen de werkwijze verwoorden:
> Je kan ‘in stapjes redeneren’ bv. 100 kg gaat 10 keer in 1 ton, 1 ton gaat 5 keer in 5 ton, dus het gewicht is met 50 vermenigvuldigd.
> Je kan onmiddellijk herleiden bv. 5 ton = 5000 kg = 50 x 100 kg.
- Laat de oplossing op verschillende manieren verwoorden: de verhouding van het gewicht van het kalfje tot het gewicht van de volwassen olifant is 1 op 50, of een volwassen olifant weegt 50 keer zoveel als een pas geboren olifant.
- Ter info: een mannelijke volwassen olifant wordt een ‘bul’ of stier genoemd, het vrouwtjesdier een koe, de baby-olifant wordt het kalf genoemd.
- Daag leerlingen uit met de vraag of de verhouding bij mensen ook zo is. Vergelijk het gemiddeld gewicht van een baby (ongeveer 3 kg) met het gewicht van een volwassen persoon.
Hoeveel betaal ik ongeveer voor de jonge kaas?

Tip: werk met een eigen kasticket of met een foto van een bedieningstoog waar de prijs per kg vermeld staat.
- Bekijk met de leerlingen het kassaticket: wat betekenen de getallen die erop staan? (ter info: PLU is een code voor groente en fruit die bedoeld is voor de administratie in de winkel, dit is hier niet relevant.)
- Bespreek welke bewerking we zouden maken als we exact rekenen.
- Bespreek de verschillende oplossingsmethodes en schattingen, motiveer leerlingen om met ronde getallen te werken.
bv. 336 g kaas is ongeveer 1/3 kg kaas — 14,75 euro is ongeveer 15 euro — 1/3 van 15 euro is 5 euro.
bv. 0,336 rond ik af naar 0,3 — 14,75 rond ik af naar 15 — 0,3 x 15 = (3 x 15) : 10 = 4,5
- Laat vluggerds op dezelfde manier de prijs voor de manchegokaas checken (bv. het ging om ongeveer ¼ kg kaas tegen ongeveer 28 euro per kg, dus ongeveer 7 euro voor dit stuk kaas).
- Laat leerlingen benoemen welke wiskundige vaardigheden ze nodig hadden om deze opgave aan te pakken: de prijzen op een ticket begrijpen, werken met gram en kg, kommagetallen afronden, tafels, hoofdrekenen, verband kommagetallen en breuken.
- Ga in op het nut van schatten bij het controleren van een rekening: je krijgt snel een beeld of de prijs kan kloppen.
De zwaarste dino was de Brachiosaurus.
Hij woog wel 80 ton.
Een dinokoek weeg 20 gram.
Hoeveel dinokoekjes wegen samen evenveel als de Brachiosaurus?
- Besteed aandacht aan een stapsgewijze manier van rekenen, bijvoorbeeld:
> 80 ton = 80 000 kg = 80 000 000 gram.
> 80 000 000 : 20 = 4 000 000 = 4 miljoen
- Bespreek met de leerlingen welke zaken nodig zijn om deze opgave te kunnen oplossen (weten hoeveel kg in een ton gaat en hoeveel g in een kg, vlot kunnen rekenen met getallen met veel nullen, weten hoeveel 1 miljoen is).
- Ter info: de Brachiosaurus was een enorm grote dino. Het was een planteneter met een nek van wel 10 meter. Laat het gewicht van de Brachiosaurus ook eens vergelijken met het gewicht van een volwassen Afrikaanse olifant (zo’n 6 ton).
Voertuigen stoten C02 uit, het gas dat de klimaatopwarming veroorzaakt. In de grafiek hieronder staat hoeveel gram CO2 elk vervoermiddel uitstoot per kilometer.
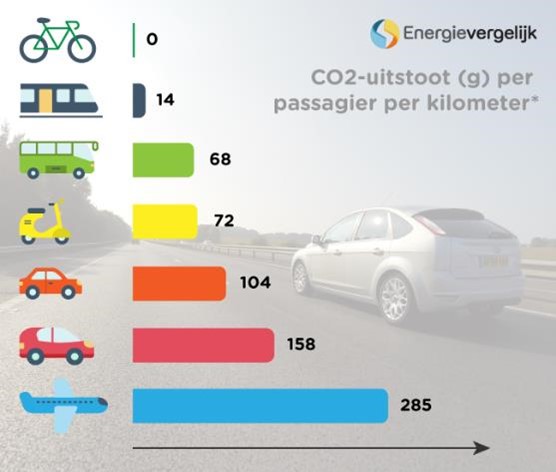
Het gezin Kos gaat met z’n vieren met het vliegtuig op reis naar Kreta. Dit is een vliegreis van ruim 2000 km (enkel). Voor hoeveel ton CO2-uitstoot zorgt deze vliegreis heen en terug? Je mag met afgeronde getallen rekenen.
- Stimuleer leerlingen om te werken met ronde getallen, hier zou je kunnen werken met 300 gram per kilometer, wat dan de bewerking 4 x 300 x 4000 gram = 4800 000 gram = 4,8 ton.
- Dit resultaat in ton maakt het mogelijk om te vergelijken met de CO2-uitstoot van een gezin op jaarbasis. Een gemiddelde personenwagen (die 15 000 km per jaar rijdt) stoot 3,4 ton CO2 . Dat betekent dat je voor het klimaat beter je vliegreis kan laten dan een heel jaar niet met de wagen rijden.
- Opmerking: De cijfers die in de opgave gebruikt worden zijn niet eenduidig, de uitstoot hangt ook af van het type vliegtuig, van het feit of het een lange of korte vlucht is,… – maar de conclusie dat vliegen veel CO2-uitstoot veroorzaakt blijft ook bij berekening met andere gegevens overeind..
- Ga eventueel in op het feit dat je de CO2-uitstoot van je vliegreis kan ‘compenseren’ via een geldbedrag.